人工智能 Java 坦克机器人系列: 神经网络，上部

神经网络概念与适合领域

神经网络最早的研究是 40 年代心理学家 Mclearcase/" target="_blank" >cculloch 和数学家 Pitts 合作提出的 ，他们提出的MP模型拉开了神经网络研究的序幕。

神经网络的发展大致经过 3 个阶段：1947～1969 年为初期，在这期间科学家们提出了许多神经元模型和学习规则，如 MP 模型、HEBB 学习规则和感知器等；60 年代末期至 80 年代中期，神经网络控制与整个神经网络研究一样，处于低潮。在此期间，科学家们做了大量的工作，如 Hopfield 教授对网络引入能量函数的概念，给出了网络的稳定性判据，提出了用于联想记忆和优化计算的途径。1984年，Hiton 教授提出 Bol tzman 机模型；1986年 Kumelhart 等人提出误差反向传播神经网络，简称 BP 网络。目前，BP网络已成为广泛使用的网络。1987年至今为发展期，在此期间，神经网络受到国际重视，各个国家都展开研究，形成神经网络发展的另一个高潮。

人工神经网络（ANN）受到生物学的启发是生物神经网络的一种模拟和近似，它从结构、实现机理和功能上模拟生物神经网络。从系统观点看，人工神经元网络是由大量神经元通过极其丰富和完善的连接而构成的自适应非线性动态系统。人工神经网络，因为生物的学习系统是由相互连接的神经元组成的异常复杂的网络，其中每一个神经元单元有一定数量的实值输入，并产生单一的实数值输出。1960 年威德罗和霍夫率先把神经网络用于自动控制研究。神经网络以其独特的结构和处理信息的方法，在许多实际应用领域中取得了显著的成效，主要应用如下：自动控制领域、处理组合优化问题、模式识别、图像处理、传感器信号处理、机器人控制、信号处理、卫生保健、医疗、经济、化工领 域、焊接领域、地理领域、数据挖掘、电力系统、交通、军事、矿业、农业和气象等领域。

回页首

攻击策略与神经网络基本结构

在 Robocode 中所有的机器人都是在指定大小的地图上移动作战，所以我们可以近似的把这些战斗的机器人看做是一些非线性移动的点。要想准确的打中对手，我们必须要知道动手的运动轨迹，也即要知道战场中每个非自身机器人点的非线性规律。在手写代码中，我们可以把敌人假想的动作都放入到攻击程序代码中，但是战场的情况和环境是不断变化的，我们不可能预测到所有的可能变化，所以拥有一个自学习，自适应的攻击系统尤为重要。本文借丹麦奥尔堡大学 Robocode 研究小组的 outRobot 机器人来分析神经网络的代码实现。

根据上面神经网络的一些特性。我们发现 Robocode 的攻击系统设计其实就是神经网络处理不确定或不知道的非线性系统的问题求解过程。

神经网络基本结构

人工神经网络由神经元模型构成，这种由许多神经元组成的信息处理网络具有并行分布结构。每个神经元具有单一输出，并且能够与其它神经元连接；存在许多（多重）输出连接方法，每种连接方法对应一个连接权系数。可把 ANN 看成是以处理单元 PE(processing element) 为节点，用加权有向弧(链)相互连接而成的有向图。令来自其它处理单元(神经元)i的信息为Xi，它们与本处理单元的互相作用强度为 Wi，i=0,1,…，n-1，处理单元的内部阈值为 θ。那么本神经元的输入为：

而处理单元的输出为：

式中，xi为第 i 个元素的输入，wi 为第 i 个元素与本处理单元的互联权重。f 称为激发函数(activation function)或作用函数。它决定节点(神经元)的输出。该输出为 1 或 0 取决于其输入之和大于或小于内部阈值 θ。

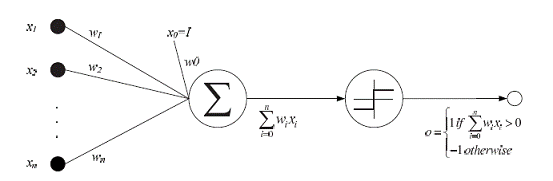
下图所示神经元单元由多个输入，i=1,2,...,n和一个输出y组成。中间状态由输入信号的权和表示，而输出为：

攻击输入输出

由上面神经网络的基本结构我们知道，设计攻击瞄准系统网络前我们必须决定为网络提供哪些参数。而且要考虑到哪些输出是合格的。在决定攻击网络系统输入数据之前，我们先来看看输出的是什么。攻击系统最终目的是提高命中敌人的概率，也即尽可能的多打中敌人，也即控制炮管在发射前转动多少度才能打中目标，所以我们的神经网络中最后输出的数据是已经计算好的炮管需要转动的角度。

在炮管指向目标前，需要计算目标状态以调整我们的炮管角度，如果目标不是固定的，神经网络的输出可以被看做是需要调整的角度。当攻击一个固定目标，神经网络不需要调整角度，直接输出零值。

Robocode 基本规则机器人移动速度在每个单位时间不可能超过8 pixels，子弹最小能达到的速度在每个单位时间是 11 pixels。我们数学三角函数计算公式求得调整角度为 sin(8/11)=47，由此可以得出最大的角度范畴是 47*2=94 度，如图所示：

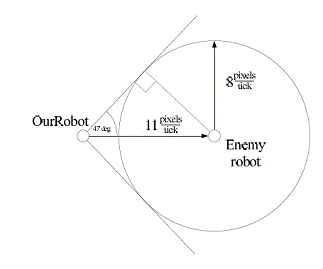
我们从图上可以看出目标在被打中前无论如何也不可能移出图中的圆锥体。这样我们可以把神经网络的输出范围缩小为 94 度或 [-47，47] 区间。

上面的 8 和 11 都是理想状态下的测试数据，在 Robocode 规则中能量不同的子弹速度是不一样的，而且射击位置的远近也同样会影响到子弹击中目标的概率。所以只有知道了射击的位置以及射击能量。神经网络才能够精确计算自身和炮管的调整角度。

由于战斗情况是千变万化的，不同的能量可能带来不同的效果。所以我们同样把能量参数并入到神经网络中，让攻击网络系统自我学习在当时的新情况下什么样的能量是最合适的。炮管调整角度是精确到了区间 [-47,47]，同样我们也可用这个方法来假定一个能量区间减少能量输出范围尽快求得好的结果。如下式，我们用距离参数来划定能量区间：

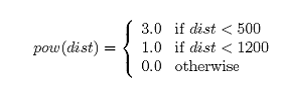
dist在此处代表目标距离，不同的距离输出不同的能量值。

在上面的输出基础上，我们来检验各种可能的输入情况，下面列出了对调整射击角度有影响的基本输入信息： 敌人相对方向(Enemy heading），Enemy velocity(敌人速度)，炮管绝对方向(Gun bearing)，距离(Distance)。我们用神经网络的输入和输出数据建立一个神经网络瞄准系统关联表示图。

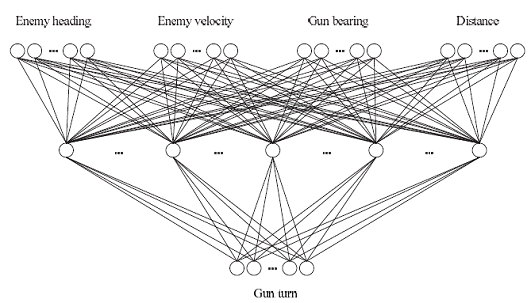
神经网络中所有计算和反馈的数据都是以二进制的方式保存在内存空间，所有的这些输入我们在神经网络用一个二进制字符来表示，如图：

在 Robocode 中我们建立一个输入数组函数 getInputs，用于处理所有相关的输入数据。

private double[] getInputs (Enemy tm, Vektor mig, Vektor ham)  {
            …
            Vektor diff = ham.substract (mig);
            double[] inputvalues = new double[36];    //创建输入数组大小为36位
            return inputvalues;
            }
            

类Vektor是一个虚构类，里面包含了机器人常用的参数和常用的处理方法。比如机器人的X坐标、Y坐标、XY之间的角度等等。它其实就是一个机器人相关信息的容器，在下面的代码实现中会介绍到 Vektor 类中的部分方法和属性。Mig 是一个包含自身机器人信息类实现，ham 包含敌人信息的类实现。

 public double getAngle ()  {
            return Math.toDegrees （(Math.atan2 (x, y))）;
            }
            //调整0-360度到[-180,180]区间
            public static double normalize (double angle)  {
            angle = mod (angle, 360.0);
            if (angle > 180)
            angle = angle - 360;
            return angle;
            }
            private static double mod (double n, double m)  {
            if (n < 0)
            return mod (n + m, m);
            if (n >= m)
            return mod (n - m, m);
            return n;
            }
            

此处根据 getAngle 由三角反正切函数得到，normalize 函数是把得到的角度规范到 [-180,180] 区间上来。

敌人相对方向最基本的信息，它告诉我们目标的相对方向。要神经网络成功计算调整角，瞄准系统需要知道在炮管指向目标时，目标是向左或向右移动。比如：目标向右直线移动，它就要给我们 90 度相对方向，瞄准系统才能比较理想的攻击到右边的目标：

int enemyRelativeHeading = (int) (tm.getHeading ());
            enemyRelativeHeading =
            (int) Vektor.normalize (enemyRelativeHeading) + 180;//设置敌人相对方向
            for (int i = 1; i < 10; i++)    {
            inputvalues[i - 1] = enemyRelativeHeading >>> 9 - i &
            0x01;//转换为二进制
            }
            

敌人相对方向这个数在 0 到 360 度之间，为了表示这些数据我们需要内存提供九个位来保存相对方向角的二进制数，通过循环把角度转换为二进制码并写入到 inputvalues 数组变量中。

敌人速度告诉我们目标以多快速度移动，要想瞄准系统知道目标的移动大概方向，就需要知道目标移动速度，这样才能计算出正确的调整角。

int enemyVelocity = (int) tm.getVelocity () + 8;
            for (int i = 1; i < 6; i++)    {
            inputvalues[i + 8] = enemyVelocity >>> 5 - i & 0x01; //转换二进制
            }
            

由于速度的范围是 [-8,8] 之间，我们共需要 17 个不同的表现值，所以内存要提供 5 个位保存速度的二进制码，inputvalues 数组变量中我们的计数在上面方向角的基础上增加 5 位。但在神经网络中我们可以不考虑负值，所以此处我们在速度的基础上加上 8，以去除负的速度对神经网络的影响。

炮管绝对方向告诉我们当前炮管应该指向哪个方向，如果炮管要指向 30 度的方向，它必须转动 (turn)30 度。这个角度类似于敌人相对方向角度，同样是 0 到 360 度之间的角度，同样需要九个二进制位来表示。

int gunBearing =
            (int) Vektor.normalize (diff.getAngle);
            gunBearing = (int) Vektor.normalize (gunBearing) + 180;
            for (int i = 1; i < 10; i++)     {
            inputvalues[i + 13] = gunBearing >>> 9 - i & 0x01;
            }
            

距离是目标的原始距离。知道目标方向、速度和距离，瞄准系统有足够多的信息猜出当子弹接近目标时，目标将到达哪个地方。这有一点要注意的地方，子弹的速度会影响到调整角度，因为距离是由速度计算得来，所以速度实际上是隐藏在距离这个输入数据之中的。只要给出距离，瞄准系统就能知道子弹的正确速度。Robocode 战场最大长高是 5000，则最大的由公式 50002 + 50002 = C2 得到 C=7071，这需要 13 个二进制位来表示。

int distanceToEnemy = (int) diff.getLength ();
            for (int i = 1; i < 14; i++)    {
            inputvalues[i + 22] = distanceToEnemy >>> 13 - i & 0x01;
            }
            

getLength() 函数即求二点间的距离函数：

    public double getLength ()   {
            return Math.hypot (x, y);
            }
            

在我们神经网络设计说明中，我们需要输出一个角度，告诉我们炮管要打中移动中的目标要转动多少。要达到这一步我们需要表示 94 度，也即二进制中的 7 位。下面是一个二进制位表示的输入输出训练例子如下：10100111000100110101110010100111110 1001110

最后 7 位(1001110)是网络给出的 36 位输入中最佳输出。也即我们要求的角度。

回页首

训练网络

神经网络结构被设计完成，有了输入、输出参数后，我们就要对网络进行训练。神经网络的训练有包括感知器训练、delta 规则训练和反向传播算法等训练，其中感知器训练是基础。

感知器和 delta 训练规则

理解神经网络的第一步是从对抽象生物神经开始,本文用到的人工神经网络系统是以被称为感知器的单元为基础，如图所示。感知器以一个实数值向量作为输入，计算这些输入的线性组合，如果结果大于某个阈值，就输出 1，否则输出 -1，如果 x 从 1 到 n，则感知器计算公式如下：

其中每个 wi 是一个实数常量，或叫做权值，用来决定输入 xi 对感知器输出的贡献率。特别地，-w0是阈值。

尽管当训练样例线性可分时，感知器法则可以成功地找到一个权向量，但如果样例不是线性可分时它将不能收敛，因此人们设计了另一个训练法则来克服这个不足，这个训练规则叫做 delta 规则。感知器训练规则是基于这样一种思路--权系数的调整是由目标和输出的差分方程表达式决定。而 delta 规则是基于梯度降落这样一种思路。这个复杂的数学概念可以举个简单的例子来表示。从给定的几点来看，向南的那条路径比向东那条更陡些。向东就像从悬崖上掉下来，但是向南就是沿着一个略微倾斜的斜坡下来，向西象登一座陡峭的山，而北边则到了平地，只要慢慢的闲逛就可以了。所以您要寻找的是到达平地的所有路径中将陡峭的总和减少到最小的路径。在权系数的调整中，神经网络将会找到一种将误差减少到最小的权系数的分配方式。这部分我们不做详细介绍，如有需要大家可参考相关的人工智能书籍。

反向传播算法

人工神经网络学习为学习实数值和向量值函数提供了一种实际的方法，对于连续的和离散的属性都可以使用。并且对训练数据中的噪声具有很好的健壮性。反向传播算法是最常见的网络学习算法。这是我们所知用来训练神经网络很普遍的方法，反向传播算法是一种具有很强学习能力的系统，结构比较简单，且易于编程。

鲁梅尔哈特(Rumelhart)和麦克莱兰(Meclelland)于 1985 年发展了 BP 网络学习算法，实现了明斯基的多层网络设想。BP网络不仅含有输入节点和输出节点，而且含有一层或多层隐(层)节点。输入信号先向前传递到隐藏节点，经过作用后，再把隐藏节点的输出信息传递到输出节点，最后给出输出结果。节点的激发函数一般选用 S 型函数。

反向传播(back－propagation，BP)算法是一种计算单个权值变化引起网络性能变化值的较为简单的方法。由于BP算法过程包含从输出节点开始，反向地向第一隐含层(即最接近输入层的隐含层)传播由总误差引起的权值修正，所以称为"反向传播"。反向传播特性与所求解问题的性质和所作细节选择有极为密切的关系。

对于由一系列确定的单元互连形成的多层网络，反向传播算法可用来学习这个多层网络的权值。它采用梯度下降方法试图最小化网络输出值和目标值之间的误差平方，因为我们要考虑多个输出单元的网络，而不是像以前只考虑单个单元，所以我们要重新计算误差E，以便对所有网络输出的误差求和:

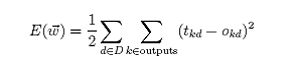
Outpus 是网络输出单元的集合，tkd 和 okd 是与训练样例 d 和第 k 个输出单元的相关输出值.

反向传播算法的一个迷人特性是：它能够在网络内部的隐藏层发现有用的中间表示:

1.训练样例仅包含网络输入和输出，权值调节的过程可以自由地设置权值，来定义任何隐藏单元表示，这些隐藏单元表示在使误差E达到最小时最有效。

2.引导反向传播算法定义新的隐藏层特征，这些特征在输入中没有明确表示出来，但能捕捉输入实例中与学习目标函数最相关的特征

Robocode代码实现

反向传播训练神经元的算法如下：

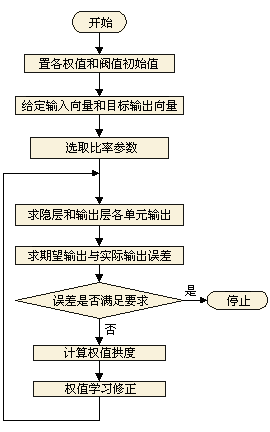
1.选取比率参数r

2.进行下列过程直至性能满足要求为止:

① 对于每一训练(采样)输入，
　　　　　　(a) 计算所得输出。
　　　　　　(b) 按下式计算输出节点的值
　　　　　　　　
　 　　　　　　　　　　　　　　　　(c) 按下式计算全部其它节点
　　　　　　　
　　　　 　 　　　　　　　(d) 按下式计算全部权值变化

② 对于所有训练(采样)输入，对权值变化求和，并修正各权值。

权值变化与输出误差成正比，作为训练目标输出只能逼近 1 和 0 两值，而绝不可能达到 1 和 0 值。因次，当采用 1 作为目标值进行训练时，所有输出实际上呈现出大于 0.9 的值；而当采用 0 作为目标值进行训练时，所有输出实际上呈现出小于 0.1 的值；这样的性能就被认为是满意的。

下面是 Robocode 中反向传播算法神经网络实现过程，把各个相关的输入信号先正向传递到隐节点，经过作用后，再把隐节点的输出信息传递到输出节点，最后给出输出结果。节点的激发函数一般选用 S 型函数。

Robocode 的 BP 算法学习过程由正向传播和反向传播组成。在正向传播过程中，输入信息从输入层经隐单元层逐层处理后，传至输出层。每一层神经元的状态只影响下一层神经元的状态。如果在输出层得不到期望输出，那么就转为反向传播，把误差信号沿原连接路径返回，并通过修改各层神经元的权值，使误差信号最小。

public class BPN {
            …
            //构造神经网络对象
            public BPN (int hidden, double lrate, int output, int input)  {
            inputNeurons = input;  //输入
            hiddenNeurons = hidden; //隐藏层
            outputNeurons = output;  //输出
            learningrate = lrate;   //学习概率
            outputValues = new double[output];
            hiddenValues = new double[hidden];
            m1 = new double[input][hidden];  //输入到隐藏层的加权
            m2 = new double[hidden][output]; //隐藏层到输出层的加权
            fillRandom (m1);
            fillRandom (m2);
            }
            

Learningrate 是学习速率，inputNeurons 是网络输入的数量，hiddenNeurons 是隐藏层单元数，outputNeurons 是输出单元数，m1 表示节点输入层到隐藏层的权值，m2 表示节点隐藏层到输出层的权值。为了让神经网络的权值更容易保存，m1、m2 放在一个序列化对象 MatrixSave 之中。

public class MatrixSave implements Serializable{
            double[][] m1;
            double[][] m2;
            public MatrixSave (double[][]m1, double[][]m2) {
            this.m1 = m1;
            this.m2 = m2;
            }
            

1.通过构造函数 BPN () 我们创建一个具有 input 个输入，hidden 个隐藏，output 个输出单元的网络。

//迭代设置网络最小权值
            public void fillRandom (double[][]matrix)  {
            Random ran = new Random ();
            for (int i = 0; i < matrix.length; i++)    {
            for (int j = 0; j < matrix[0].length; j++)  {
            matrix[i][j] = ran.nextDouble () * 2 - 1;
            }
            }
            }
            

2.fillRandom 是初始化所有的网络权值为小的随机值，即 -1 和 1 之间的随机数。

3.把输入沿网络正向传播,把实例输入网络：输入信号先向前传递到隐藏节点hiddenNeurons，经过加权作用后，利用神经网络的计算函数公式常规 S 激励函数求得隐藏节点的激励数，再把隐藏节点的输出信息传递到输出节点，同样用激励函数求得输出激励，最后给出输出结果并计算网络中每个单元的输出output.

激发函数一般具有非线性特性。常用的非线性特性如图所示，分述于下： 一种二值函数可由下式表示：

对于这种模型，神经元没有内部状态，激发函数为一阶跃函数，如图 a 所示。这时，输出为：

Sigmoid 型激发函数称为西格莫伊德(Sigmoid)函数，简称 S 型函数，其输入输出特性常用对数曲线或正切曲线等表示。这类曲线反映了神经元的饱和特性。S 型函数是最常用的激发函数，它便于应用梯度技术进行搜索求解。一种常规的 Ｓ 形函数见图,可由下式表示如图 b：

常用双曲正切函数来取代常规 Ｓ 形函数，因为 Ｓ 形函数的输出均为正值，而双曲正切函数的输出值可为正或负。双曲正切函数如下式所示如图 c：

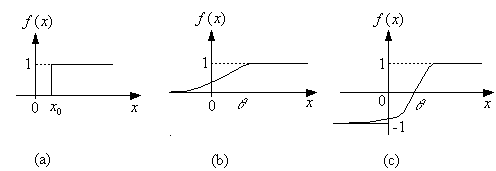
由上面的激励函数求得如下：

  public double[] calculate (double[]inputValues)   {
            for (int i = 0; i < hiddenNeurons; i++)     {
            double sum = 0;
            //设置输入层到隐藏层的网络权值
            for (int j = 0; j < inputNeurons; j++) 	  {
            sum += m1[j][i] * inputValues[j];
            }
            hiddenValues[i] = 1 / (1 + Math.exp (-(sum))); //计算隐藏层
            }
            //计算隐藏层到输出层的网络权值
            for (int i = 0; i < outputNeurons; i++)     {
            double sum = 0;
            for (int j = 0; j < hiddenNeurons; j++)   {
            sum += m2[j][i] * hiddenValues[j];
            }
            outputValues[i] = 1 / (1 + Math.exp (-(sum)));
            }
            return outputValues;
            }
            

4.把训练样例 TrainingExample 输入网络，并计算网络中每个单元的输出，然后使误差沿网络反向传播，并分别计算网络的每个输出单元 outputNeurons 和隐藏单元 hiddenNeurons 的误差项,最后更新每个网络权值。训练样例 TrainingExample 是序偶 <inputvalues,targetvalues> 的集合，即网络输入值向量和目标输出值。threshold 为网络阀值。

public void learn (TrainingExample[]te, double threshold)  {
            double[] outputError = new double[outputNeurons]; //输出单元误差
            double[] hiddenError = new double[hiddenNeurons]; //隐藏单元误差
            double[] inputValues;
            double outputs[]; //训练样例中的输入值
            double targets[]; //训练样例中的目标值
            for (int tal = 0; tal < (int) threshold; tal++)
            

根据正向传播计算输出单元

  outputs = calculate (inputValues);
            //利用神经网络加权计算输出单元误差outputError
            for (int j = 0; j < outputs.length; j++)   {
            outputError[j] =outputs[j] * (1 - outputs[j]) * (targets[j] - outputs[j]);
            }
            

利用神经网络加权计算隐藏单元误差hiddenError

    for (int j = 0; j < hiddenValues.length; j++)     {
            double sum = 0;
            for (int k = 0; k < outputNeurons; k++)		  {
            sum += m2[j][k] * outputError[k];
            }
            hiddenError[j] = hiddenValues[j] * (1 - hiddenValues[j]) * sum;
            }
            

分别更新网络权值m1，m2

 //更新网络权值m1
            for (int l = 0; l < m1.length; l++)	      {
            for (int o = 0; o < m1[0].length; o++)		  {
            m1[l][o] = m1[l][o] + learningrate * hiddenError[o] * inputValues[l];
            }
            }
            //更新网络权值m2
            for (int l = 0; l < m2.length; l++)     {
            for (int o = 0; o < m2[0].length; o++)  {
            m2[l][o] =m2[l][o] +learningrate * outputError[o] * hiddenValues[l];
            }
            }
            

完成了我们的神经网络机器人结构的初步构建，我们就要开始训练网络，让我们的机器人在不断的学习、自我适应过程中完成进化，找到最终要输出的最佳结果。在这里有两个办法训练可以我们的网络：分别是离线学习和在线学习。

回页首

离线学习(off-line learning）

一般人工智能的机器人的训练过程都要经过一个漫长的过程才有可能找到最优化的结果。但 Robocode 的规则以及电脑 CPU 不可能给出很多的时间让我们的神经网络机器人运行。所以机器人必须在游戏运行之外学习。也即要使用离线学习方法，我们在 Robocode 运行中收集计算有用数据并把它们保存到文件当中。新的数据收集都是以保存在文件中的数据为依据。比如：新的加权是根据以前保存的加权文件来构造的随机加权集合。

public class Learn {
            public static void main (String[]args)   {
            BPN net = new BPN (27, 0.45, 15, 36);
            net.loadWeights (new File ("weights.dat"));
            TrainingExample[] te = loadTE (new File ("danivan.txt"));
            performance (net, te); //判断最佳的网络
            net.learn (te, Integer.parseInt (args[0])+ 0.0); //反向传播学习
            performance (net, te);
            net.saveWeights (new File ("weights.dat"));
            }
            }
            

上式通过 loadWeights，loadTE 分别读取保存的加权集及训练示例，利用反向传播学习方法来训练示例。一定时间内数据通过网络，并依据我们的设想运作，当所有的训练示例都通过了反向传播算法，并判断网络中的最佳结果，加权集将保存到磁盘中，这些加权集将用于 Robocode 的战斗，作为机器人的瞄准系统参数。这里我们要注意不要使用大量的隐藏神经单元，因为这样有可能会得到一个带有风险的网络，以至网络可能只接受精确的示例导致没有理想结果。

  //判断最佳的网络
            public static boolean performance (BPN net, TrainingExample te) {
            boolean b = false;
            double[] output = net.calculate (te.getInputValues ());
            double[] target = te.getTargetValues ();
            for (int i = 0; i < output.length; i++)    {
            if (!((output[i] > 0.5 ? 1.0 : 0.0) == target[i]))	  {
            b = false;
            break;
            }
            else  {
            b = true;
            }
            }
            return b;
            }
            

回页首

实时学习进化(Online-Learning)

实时学习，即在 Robocode 的运行当中，让我们的机器人进行神经网络学习。它的原理和离线学习是一样的，只是它是即时学习即时利用输入的数据更新加权值。而离线学习是把权值保存到磁盘当中。每次炮管的开火在线学习都会做如下的动作：

1.输入X到神经网络并计算输出

2.调整输出角度，发射子弹

3.保存射击数据

4.从开火中等待是否击中事件返回

5.从保存的数据和打击事件构造训练示例

6.用反向传播算法训练示例神经网络

第 5 步我们用保存的数据和到达的开火事件构造训练示例。使用这些数据我们能知道目标精确的移动，并且能构造一个算法计算在当时的环境和时间中子弹最优的攻击线路。我们通过训练示例计算得到所有的输入和输出，当我们有了这些关于射击的最优数据，我们就能更新网络中的加权集。

  //在线学习
            public OnlineLearn (BPN net, File weights, File trainingExamples)   {
            TrainingExample[]te = loadTE (trainingExamples);
            net.learn (te, 1.0);
            }