计算机英语：“与”函数

  The AND function can be illustrated by the fol lowing analogy. The members of group A are Bob, Charley, and Dick. Note that the names in this group combined by the conjunction“and”．That means group A equals the presence of Bob and Charley and Dick. This may be symbolized as     
　　A=B•C•D 
　　A is true (group A is present) when B istrue(Bob is present)，AND C is true (Charley is present)．AND D is true (Dick is present). A is not trueif anv one (or more) of the members are absent.

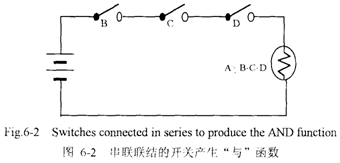
　　The circuit in Figure 6-2 can be used to producethe AND function of the above example. The lightindicates that group A is present only when all mcm-bers of the group are present. A logic circuit produc-ing the AND function is called an AND gate and issymbolized in Figure 6-3．

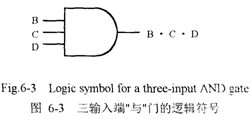
　　Figure 6-4(a) shows the logic symbol for a twoinput AND gate. The function (A-B) is producedwhen A is true AND B is true. In order to show all ofthe conditions that may exist at the input and outputof a logic gate, truth tables are used. Because thereare two inputs and each input has two possible states(true and false)，the number of possible conditions at, I,Ile nput would be 2 raised to the second power (22)，or 4．The truth table for a two- input AND gate isshown in Figure 6-4(b) Note that condition 4 is theanly one in which all of the inputs are true so that theAND function is produced and a true output appears。

　　AND gates may have two or more inputs．Figure0-5 shows a three-input AND gate and its truth tableOncs(I)and zcros(O) are used for the alucs of theN ariables．Because three variables are used. eight：onditions exist(23=8)．Condition 8 is the onk onethat will produce a true output（I）because all of theinput variables are true(equal to I)．

原文转自：http://www.ltesting.net