关于描述性统计分析

在数据分析的时候，一般首先要对数据进行描述性统计分析（Descriptive Analysis），以发现其内在的规律，再选择进一步分析的方法。描述性统计分析要对调查总体所有变量的有关数据做统计性描述，主要包括数据的频数分析、数据的集中趋势分析、数据离散程度分析、数据的分布、以及一些基本的统计图形。

    （1）数据的频数分析：在数据的预处理部分，我们曾经提到利用频数分析和交叉频数分析来检验异常值。此外，频数分析也可以发现一些统计规律。比如说，收入低的被调查者用户满意度比收入高的被调查者高，或者女性的用户满意度比男性低等。不过这些规律只是表面的特征，在后面的分析中还要经过检验。

    （2）数据的集中趋势分析：数据的集中趋势分析是用来反映数据的一般水平，常用的指标有平均值、中位数和众数等。各指标的具体意义如下：

    平均值：是衡量数据的中心位置的重要指标，反映了一些数据必然性的特点，包括算术平均值、加权算术平均值、调和平均值和几何平均值。

    中位数：是另外一种反映数据的中心位置的指标，其确定方法是将所有数据以由小到大的顺序排列，位于中央的数据值就是中位数。

    众数：是指在数据中发生频率最高的数据值。

    如果各个数据之间的差异程度较小，用平均值就有较好的代表性；而如果数据之间的差异程度较大，特别是有个别的极端值的情况，用中位数或众数有较好的代表性。

    （3）数据的离散程度分析：数据的离散程度分析主要是用来反映数据之间的差异程度，常用的指标有方差和标准差。方差是标准差的平方，根据不同的数据类型有不同的计算方法。

    （4）数据的分布：在统计分析中，通常要假设样本的分布属于正态分布，因此需要用偏度和峰度两个指标来检查样本是否符合正态分布。偏度衡量的是样本分布的偏斜方向和程度；而峰度衡量的是样本分布曲线的尖峰程度。一般情况下，如果样本的偏度接近于0，而峰度接近于3，就可以判断总体的分布接近于正态分布。

    （5）绘制统计图：用图形的形式来表达数据，比用文字表达更清晰、更简明。在SPSS软件里，可以很容易的绘制各个变量的统计图形，包括条形图、饼图和折线图等。

示例  SIM手机描述性统计分析

为简化起见，我们只分析SIM手机用户满意调查中的两个变量：“总体感知质量”和“总体满意度”变量。

（1）数据的频数分析

用SPSS软件的频数分析可以很容易地画出两个变量的频数图：

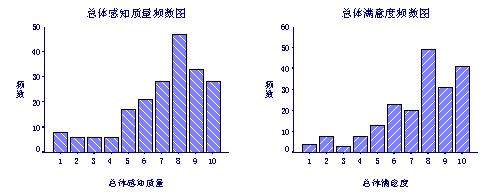javascript:if(this.width>740)this.width=740" border=undefined>

 两个变量的频数图表明：大部分被调查者对SIM手机的质量评价较高，总体感觉比较满意，打分在8－10分之间。

（2）数据的集中趋势分析

    利用SPSS的描述性统计分析，计算SIM手机“总体感知质量”和“总体满意度”的平均值、中位数和众数：

共有200个（N）被调查者参与了SIM手机调查；总体感知质量均值（Mean）7.11分、中位数（Median）8分、众数（Mode）8分；总体满意度均值7.43分、中位数8分、众数8分，与前面的频数分析结果一致。

    （3）数据的离散程度和分布分析：

    同样利用SPSS软件的描述性统计分析，可以得出SIM手机的离散程度和分布指标：

“总体感知质量”变量的标准差（Std. Deviation） 2.36、方差（Variance） 5.56；“总体满意度”标准差2.29、方差5.25，说明不同样本对两个变量打分的差异程度不大，或者说不同样本对SIM手机评价的差异不大。“总体感知质量”变量的偏度（Skewness）-0.961、峰度（Kurtosis）0.358；“总体满意度”变量偏度-0.988、峰度0.437，说明数据不符合正态分布

原文转自：http://www.ltesting.net