测试中的随机性(5)

　　我每隔 10 个值就用模数 (%) 运算符打印一个新行，只是为了保持输出整齐。来自平均值为 68.0 英寸、标准偏差为 6.0 英寸的正态分布随机身高通过 Gaussian.NextGaussian2 方法的调用返回，我稍后将对此详细说明。我通过监控小于 56 英寸或大于 80 英寸的值来跟踪非正常值。这些值是高于或低于平均值 68.0 英寸两个标准偏差(6.0 * 2 = 12.0 英寸)的值。据统计，随机生成值超过平均值两个正(或负)标准偏差的概率大约有 5%。因此，如果生成 100 个随机身高(就像我现在这样)，则可以预期约有 5 个非正常值。如果得出的非正常值远多于或远少于 5 个，则就需要仔细检查代码。请注意，在图 1 所示的运行示例中，我刚好得到 5 个非正常值，这使我更加确信我的随机生成的身高数据点实际上是正态分布的。

　　Box-Muller 算法隐含的原理非常深奥，但结果却是相当简单。如果您在 [0,1) 值域内有两个一致的随机数字 U1 和 U2(如本专栏中第一部分所述)，则您可以使用以下两个等式中的任一个算出一个正态分布的随机数字 Z：

　　正态值 Z 有一个等于 0 的平均值和一个等于 1 的标准偏差，您可使用以下等式将 Z 映射到一个平均值为 m、标准偏差为 sd 的统计量 X：

　　以 NextGaussian 方法实现高斯类的最简单方法由图 6 中的代码表示。

　　我使用的是 Math.Cos 版本，但我本完全可以轻松地使用 Math.Sin 版本。该实现代码虽然可行，但效率很低。由于 Box-Muller 算法可利用 sin 或 cos 中的任一个函数计算正态分布的 Z 值，因此我倒不如同时计算两个 Z 值，保存第二个 Z 值，然后在第二次调用 NextGaussian 方法时可以检索所保存的值。此类实现方法如图 7 所示。

　　尽管该方法可行性很好，但也存在一些低效性。使用 Math.Sin、Math.Cos 和 Math.Log 方法进行计算会降低性能。一种提高效率的巧妙方法是使用数学技巧。如果您检查一下 R 和 θ 的定义，会发现它们与某单位圆内某随机点的极坐标相对应。该数学技巧就是计算单位正方形内某随机点的坐标(避免了调用 Math.Sin 和 Math.Cos 方法)并确定该随机点是否在单位圆范围内。如果是这样，我们就可以使用这组坐标;如果不是这样，则我们可计算一组新的随机坐标，然后重试一次。约有 78% 的随机生成坐标都在单位圆范围内，这提供了更好的性能，但显然要影响到清晰性。

　　图 8 中例示了单位正方形技巧。Box-Muller 基本算法将选择一个极坐标为 (R, θ) 并保证在单位圆范围内的点。您也可以在包围单位圆的单位正方形内选择矩形坐标;点 (x1, y1) 在单位圆范围内，但是点 (x2, y2) 则在单位圆范围之外。图 9 说明了单位正方形方法的实现。

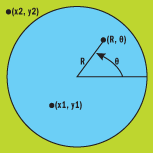
　　图 8 单位正方形技巧

　　在软件测试场景中，性能通常不是主要的考虑因素，因此我所提到的三种实现方法都适用。但在软件开发中，特别是在进行模拟时，性能就成为一个主要问题。尽管 Box-Muller 算法执行起来既高效又相对简单，但是也有其他替代算法可生成正态/高斯伪随机数字。有一种高效的替代方法称为 ziggurat 方法。

　　总结

　　让我进行一下简单总结。生成随机测试用例输入数据是基本的软件测试技能。.NET Framework 包含一个 System.Random 类，可用于生成某一特定值域内的统一分布的整数型或浮点型伪随机数字。需要注意的主要问题就是要确保正确指定值域的端点值。

　　可使用 Wald-Wolfowitz 检验方法来分析包含两个符号的模式以证明它是随机生成的模式。您可使用此检验方法分析随机测试用例输入数据或分析所测试系统的输出数据。

　　最佳通用混排算法称为 Fisher-Yates 算法。它非常简单并且几乎不需要使用另一种方法。但即使正确算法中存在一丝微小偏差都可能导致算法看似正确但却存在重大错误。

原文转自：http://www.uml.org.cn/Test/200611225.htm