等价类分法 新解

　　等价类分法

　　1.1 等价类分法的基本概念

　　等价类分法是将测试空间划分成若干个子集，并且满足每个子集中的任一数据对揭露程序中的缺陷都是等价的，这些子集就叫做等价类或者叫等价子集。

　　比如一个程序的输入数据满足 0

　　1 ～99中的任一数据和其他数据都是等价的，比如使用了2来进行测试，那么可以假定数据2测试通过的话，1～99中的其他数据也能测试通过。

　　等价类分法可以用来对一些不能穷举的集合进行合理分类，从各个等价类中选出有代表性的数据进行测试，从而保证设计出来的设计用例具有一定的代表性和一定范围内的完整性，有效地缩减测试用例的数量。

　　等价类实际上是符合测试空间划分原则的一种特殊划分形式，即划分完后的子集里的可测数据是等价的，而测试空间划分原则则是要求里面有一个可测数据测试通过能够代表其他测试数据在满足选取概率条件下也都可以通过。等价类选取测试数据时可以选取等价类中的任意数据作为测试数据，而测试空间划分原则划分的子集一般是选择指定的数据作为测试数据，如果按测试空间划分原则划分后的子集刚好成为了等价类才可以选择里面的任一数据作为测试数据。

　　1.2 等价类的几种类型

　　在现实情况中，由于缺陷的可能情况非常多，一个子集中的数据对某种缺陷是等价的，但对另外一种缺陷可能又是不等价的。所以把等价类分为弱等价类、强等价类、理想等价类三种类型。

　　1、弱等价类

　　弱等价类是考虑某个单一缺陷情况下的等价情况，子集里所有数据在这种缺陷假设下是等价的，并且划分成的几个等价类能够覆盖整个测试空间的单一缺陷。比如以下一段程序：

　　void Func(unsigned int x)

　　{

　　if ( x > 10 )

　　{

　　Func1();

　　}

　　else

　　{

　　Func2();

　　}

　　}

　　我们可以将数据划分为两个等价类，0~10为1个等价类，大于 10的数据为1个等价类，在考虑“>”号误写成“<”号这种缺陷的情况下，这两个等价集中的数据都是等价的，比如0～10这个等价类中，使用 0或使用10来进行测试都能发现缺陷。这两个等价类中各自抽取一个测试数据进行测试，都能代表其他数据揭示出“>”号误写成“<”号这种缺陷来，因此整个测试空间都被覆盖了。

　　2、 强等价类

　　强等价类是在多个缺陷假设前提下，各个等价类中的可测数据在单个或多个缺陷假设下是等价的，并且划分的各个等价子集中各自取一个测试数据可以覆盖整个测试空间的多个缺陷情况。

　　再考虑前面弱等价类中的例子程序，出错的可能性有那些呢?除了大于号会错写成小于号外，实际上还有可能写成大于等于号，10有可能写成1或100等大于10或小于10的数，为方便描述以错写成1和100为例，事实上错误成其他数和错写成1和100是等价的。这样将各种可能出错的情况组合起来，程序中的判断条件有可能有以下12种情况：

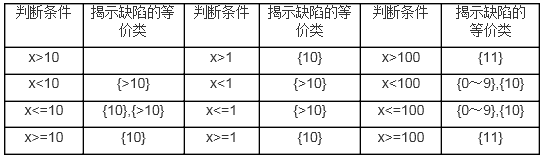
　　考虑0～10这个集合，在误写成中间一列条件中情况下，里面的数据并不等价，比如误写成x>1的情况下，使用1做测试和使用2做测试揭示缺陷是不同的，使用1做测试发现不了缺陷，但使用2测试就能发现缺陷。

　　在判断条件误写成x>=10条件下，10和0~9中的任一数据也不等价，并且使用大于10的数据也无法揭示出条件错写成x>=10这个缺陷，因此整个测试空间的多个缺陷无法被已划分的两个等价类来覆盖，10需要单独划分成一个等价类。

　　这样将数据划分成三个等价类{0～9}、{10}、{大于10的数据}，再看看这三个等价类是否可以覆盖表中各种出错情况，显然在x>100和x>=100两种情况下，大于10的数据集合中的数据是不等价的，使用大于100的数据不能揭示出缺陷，但使用大于10小于100的数据却能揭示出缺陷，因此需要对大于10的数据再划分等价类，实际上只要将边界值 {11}划一个单独的等价类就可以了。

　　这样总共得到四个等价类{0～9}、{10}、{11}、{大于 11的数据}，从这四个等价类中各取一个数据的话就可以将以上列出的所有可能的缺陷情况都揭示出来，但是各个等价类并不是对所有缺陷都等价的，这种划分的等价类由于可以将各种缺陷情况覆盖到，把它叫叫做强等价类。

原文转自：http://www.uml.org.cn/Test/201205143.asp