查τ分布表,取α=0.05,自由度15-1=14,查表得:τ(1-α)(n-1)=1.7613。
因τ =1.572<1.7613,故未落入拒绝域,原假设H0(u≤3mg/L)成立,即认为该厂排放的废水中的BOD含量符合规定要求。
类似地,其他环境保护与污染排放活动,通过监视或测量后需要进行分析判断,以确定是否达到要求。
三、职业健康安全管理中的事故发生率预测
这一管理体系运行中笔者尚未发现应用“假设检验”的典型事例,但以概率预测的方法,制订安全目标或事故预防措施的有不少。比如:用以往的事故记录,推断事故发生概率,预测事故发生,采取必要的防患措施。这在职业健康安全管理中常常遇到。
有关统计理论告知,事故的发生数,一般服从泊松分布,即一定时间或一定区域内或某一特定单位内的事故发生次数的概率以某一参数λ(特定单位一定时间内的平均值)按一定的统计规律计算。在安全管理中需要按此分布公式,根据历史的记录,进行事故发生概率的分析与考察,使领导和员工心中有数,并积极采取必要的防患措施,防止事故发生。GB/T28001-2001标准《职业健康安全管理体系 规范》的4.5.1中的规定:“被动性的绩效测量,监视事故、疾病、事件和其他不良职业健康安全绩效的历史证据;――记录充分的监视和测量的数据和结果,以便于后面的纠正和预防措施的分析。”故,这也是贯彻执行标准的需要,在此不妨举例如下。
如:某矿业公司每季发生安全事故数X服从泊松分布,按历史的事故记录,公司每季度平均发生1.2起安全事故。故X服从λ=1.2的泊松分布。
泊松分布的概率公式为:
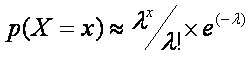
(x=0,1,2,……)。
考察或预测一个季度中发生0起,1起,2起,到7起事故的概率,为实施预防措施获取必要的信息和基础资料。
将λ=1.2,x=0~7分别代入上述公式,并列表如下:
x 0 1 2 3 4 5 6 7
p 0.301 0.362 0.216 0.087 0.026 0.006 0.002 0.000
上述统计表明:该公司每季发生1起事故的概率为最大,达0.362。但2起和3起的概率徒然下降,3起以后的概率在小数点2位,发生7起的概率几乎为0。因此,对安全事故的预防措施应着眼于发生1至2起事故,过多或过强地采取预防措施将会明显增加不必要的成本。这就是统计分析所要达到的目的。
一些企业/组织,对贯彻实施GB/T19001-2000 IDT ISO9001:2000中的8.4“数据分析”和8.1中“这应包括对统计技术在内的适用方法及其应用程度的确定”条文感到有困惑。其实这些企业/组织中存在着大量的可分析利用的数据,只是由于本身的人员条件不具备而没能有效地开展。有的则是为了应付现场审核,搞几张毫无意义的“排列图”、“因果图”,算是有了“统计技术的应用”。放着那些大量可利用的产品质量特性数据而不分析利用,也算是种资源浪费,感到可惜。纠正措施和对策方案的方向是什么?笔者认为,按标准中“6.2”条款要求实施,即适当地配置必要的人力资源和通过教学培训等措施,使统计技术的应用取得满意的成效。也使“管理体系”标准应用的有效性,得到实实在在的体现。
文章来源于领测软件测试网 https://www.ltesting.net/










