P为规定的不合格品率;
N为样本容量。
显然,μ未落入拒绝域中,不能拒绝原假设,即应允许该批产品交货。
这一例子又一次证明了,按百分比抽样判定交货的不合理性。
二、环境管理排污监测中的“假设检验”
GB/T24001—2004 idt ISO14001:2003中的4.5.1“监测和测量”要求对可能具有的重大环境影响的运行与活动的关键特性进行例行“监测和测量”并对“组织环境目标和指标符合情况进行跟踪分析。”其关键特性的监测测量必然会涉及数据的分析、检验与预测。比如:环境管理中对“水、气、声、渣”类污染排放指标监测和测量往往通过取样来判定一段时间的排污是否符合国家排放标准。特别是未建立控制图进行控制与分析的状况下,有必要对一段时间的监测数据进行假设检验。
例如:某有机化工厂地处II类地表水环境质量标准要求,排放的废水中的生物需氧量(BOD)不得超过3mg/L。废水中的BOD含量一般来说,近似服从正态分布。该企业在投产之初的半个月中,对废水中的BOD进行每日监测测量。15天的监测测量记录如下:
3.0; 3.7; 3.5; 3.4; 2.9; 3.5; 3.3;
3.1; 3.2; 2.5; 3.0; 2.9; 3.6; 2.7; 2.8。单位为mg / L 。
要问在总体上(即15天的总体情况)是否符合规定要求?并在α=0.05水平上判定是否符合Ⅱ类地表水环境质量标准?
解:如果总体排放符合Ⅱ类地表水环境质量标准,则均值u≤3mg / L,否则u>3mg /L
故设立假设:H0(u≤3) ;H1(u>3)。由于未告知总体的标准偏差σ,用样本标准偏差S替代,并按统计理论选用τ检验判定。根据15天的样本数,求得日平均值x=3.14;S=0.345;
代入检验统计量公式:
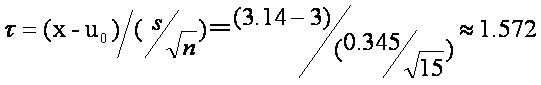
式中u0已知,即3mg/L;n为天数。
根据上述假设:H0(u≤3); H1(u>3)。知拒绝域为:{τ >τ(1-α)(n-1)}
文章来源于领测软件测试网 https://www.ltesting.net/










