低
平均
2->3
平均
平均
平均
4 or more
平均
高
高
表3 复杂性分配
一旦确定了常量的值,我们可以用这些数值计算每类的加权平均方法数(WMC)。
加权平均方法数(WMC)将会联合TLC、NOC 、DIT进行计算。
我们对这些不同形态的数据进行了归约,综合形成下面形式一个方程式。在方程式中,
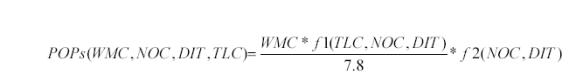
f1 计算整个系统的规模, f2计算通过重用的影响。我们开始有了一个相当小规模的数据点集合,我们用jack-knifed方法进行数据分析。我们将拿出一小百分比数据进行查证确认,其他剩余的部分进行归约(按上面的方程式),接着对比衰退计算结果和经过提出查证确认情况。我们再三重复地做,用不同的例子不断地做,直到方程式的集合能得到最好的变更系数。我们用来做归约的工具是Jandel提供得SigmaPlot。
我们的数据显示了很好的相关性,变更系数在我们采用的例子中变化范围为5~19%内。我们知道研究到今天这些结果只是初步地给了一个数据总量。研究还要进一步进行,需要收集其他类型的软件和用其他开发语言开发的应用程序的数据。
POPs 计算例证
理解了什么是POPs和它是怎么形成的,很明显下一步问题是它作为一个估计工具怎么样使用。一些POPs计算需要的信息可能是需求分析阶段没充分清楚的信息。然而,我们有可以采用的方法来合理估计计算POPs需要的参数。 下面一个例子来自[17]。利用项目提供的信息和一个面向对象度量工具,我们将演示怎么样进行POPs 计算。开发的软件是个OO Case 工具。它是用Smalltalk 开发的,有36个类和1040个方法。软件开发团队的生产力高于平均值,他们有大量的软件开发经验。
第一步是计算WMC。我们知道平均每类的方法是29(1040/36)。虽然我们不清楚这些方法的类别上的分布情况,我们可以用我们在研究过程中确定的百分比来计算:
文章来源于领测软件测试网 https://www.ltesting.net/










